JavaScript数据结构和算法之图和图算法

图的定义

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

有向图

有向边：若从顶点Vi到Vj的边有方向，则称这条边为有向边，也成为弧(Arc)，用有序偶<Vi,Vj>来表示，Vi称为弧尾，Vj称为弧头。

无序图

无向边：若顶点Vi到Vj之间的边没有方向，则称这条边为无向边(Edge)，用无序偶(Vi,Vj)来表示。

简单图

简单图：在图结构中，若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图。

图类

表示顶点

创建图类的第一步就是要创建一个Vertex类来保存顶点和边。这个类的作用和链表、二叉搜索树的Node类一样。Vertex类有两个数据成员：一个用于标识顶点，另一个表明是否被访问过的布尔值。分别被命名为label和wasVisited。

function Vertex(label){

    this.label = label;

}

我们将所有顶点保存在数组中，在图类里，可以通过他们在数组中的位置引用他们

表示边

图的实际信息都保存在“边”上面，因为他们描述了图的结构。二叉树的一个父节点只能有两个子节点，而图的结构却要灵活得多，一个顶点既可以有一条边，也可以有多条边和它相连。

我们将表示图的边的方法成为邻接表或者邻接表数组。它将存储由顶点的相邻顶点列表构成的数组

构建图

定义如下一个Graph类：

function Graph(v){

    this.vertices = v;//vertices至高点

    this.edges = 0;

    this.adj = [];

    for(var i =0;I<this.vertices;++i){

        this.adj[i] = [];

        this.adj[i].push('');

    }

    this.addEdge = addEdge;

    this.toString = toString;

}

这个类会记录一个图表示了多少条边，并使用一个长度与图的顶点数来记录顶点的数量。

function addEdge(){

    this.adj[v].push(w);

    this.adj[w].push(v);

    this.edges++;

}

这里我们使用for循环为数组中的每个元素添加一个子数组来存储所有的相邻顶点，并将所有元素初始化为空字符串。

图的遍历

深度优先遍历

深度优先遍历(DepthFirstSearch)，也有称为深度优先搜索，简称为DFS。

比如在一个房间内寻找一把钥匙，无论从哪一间房间开始都可以，将房间内的墙角、床头柜、床上、床下、衣柜、电视柜等挨个寻找，做到不放过任何一个死角，当所有的抽屉、储藏柜中全部都找遍后，接着再寻找下一个房间。

深度优先搜索：

深度优先搜索就是访问一个没有访问过的顶点，将他标记为已访问，再递归地去访问在初始顶点的邻接表中其他没有访问过的顶点

为Graph类添加一个数组：

this.marked = [];//保存已访问过的顶点

for(var i=0;i<this.vertices;++i){

    this.marked[i] = false;//初始化为false

}

深度优先搜索函数：

function dfs(v){

    this.marked[v] = true;

    //if语句在这里不是必须的

    if(this.adj[v] != undefined){

        print("Visited vertex: " + v );

        for each(var w in this.adj[v]){

            if(!this.marked[w]){

                this.dfs(w);

            }

        }

    }

}

广度优先搜索

广度优先搜索（BFS）属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。

广度优先搜索从第一个顶点开始，尝试访问尽可能靠近它的顶点，如下图所示：

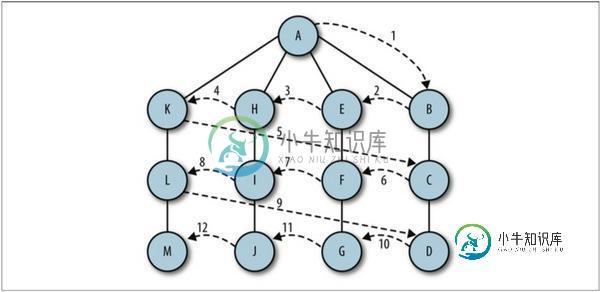
其工作原理为：

 1. 首先查找与当前顶点相邻的未访问的顶点，将其添加到已访问顶点列表及队列中；
 2. 然后从图中取出下一个顶点v，添加到已访问的顶点列表
 3. 最后将所有与v相邻的未访问顶点添加到队列中
下面是广度优先搜索函数的定义：

function bfs(s){

    var queue = [];

    this.marked = true;

    queue.push(s);//添加到队尾

    while(queue.length>0){

        var v = queue.shift();//从队首移除

        if(v == undefined){

            print("Visited vertex: " + v);

        }

        for each(var w in this.adj[v]){

            if(!this.marked[w]){

                this.edgeTo[w] = v;

                this.marked[w] = true;

                queue.push(w);

            }

        }

    }

}

最短路径

在执行广度优先搜索时，会自动查找从一个顶点到另一个相连顶点的最短路径

确定路径

要查找最短路径，需要修改广度优先搜索算法来记录从一个顶点到另一个顶点的路径，我们需要一个数组来保存从一个顶点操下一个顶点的所有边，我们将这个数组命名为edgeTo

this.edgeTo = [];//将这行添加到Graph类中

//bfs函数

function bfs(s){

    var queue = [];

    this.marked = true;

    queue.push(s);//添加到队尾

    while(queue.length>0){

        var v = queue.shift();//从队首移除

        if(v == undefined){

            print("Visited vertex: " + v);

        }

        for each(var w in this.adj[v]){

            if(!this.marked[w]){

                this.edgeTo[w] = v;

                this.marked[w] = true;

                queue.push(w);

            }

        }

    }

}

拓扑排序算法

拓扑排序会对有向图的所有顶点进行排序，使有向边从前面的顶点指向后面的顶点。
拓扑排序算法与BFS类似，不同的是，拓扑排序算法不会立即输出已访问的顶点，而是访问当前顶点邻接表中的所有相邻顶点，直到这个列表穷尽时，才会将当前顶点压入栈中。

拓扑排序算法被拆分为两个函数，第一个函数是topSort()，用来设置排序进程并调用一个辅助函数topSortHelper()，然后显示排序好的顶点列表

拓扑排序算法主要工作是在递归函数topSortHelper()中完成的，这个函数会将当前顶点标记为已访问，然后递归访问当前顶点邻接表中的每个顶点，标记这些顶点为已访问。最后，将当前顶点压入栈中。

//topSort()函数

function topSort(){

    var stack = [];

    var visited = [];

    for(var i =0;i<this.vertices;i++){

        visited[i] = false;

    }

    for(var i = 0;i<this.vertices;i++){

        if(visited[i] == false){

            this.topSortHelper(i,visited,stack);

        }

    }

    for(var i = 0;i<stack.length;i++){

        if(stack[i] !=undefined && stack[i] != false){

            print(this.vertexList[stack[i]]);

        }

    }

}

//topSortHelper()函数

function topSortHelper(v,visited,stack){

    visited[v] = true;

    for each(var w in this.adj[v]){

        if(!visited[w]){

            this.topSortHelper(visited[w],visited,stack);

        }

    }

    stack.push(v);

}